publications

2025

1. 

   How compositional generalization and creativity improve as diffusion models are trained

   Alessandro Favero , Antonio Sclocchi, Francesco Cagnetta , and 2 more authors

   2025

2. 

   Probing the Latent Hierarchical Structure of Data via Diffusion Models

   Antonio Sclocchi, Alessandro Favero , Noam Itzhak Levi , and 1 more author

   In The Thirteenth International Conference on Learning Representations , 2025

3. 

   A phase transition in diffusion models reveals the hierarchical nature of data

   Antonio Sclocchi, Alessandro Favero , and Matthieu Wyart

   Proceedings of the National Academy of Sciences, 2025

   Abs PDF

   

   The success of deep learning is often attributed to its ability to harness the hierarchical and compositional structure of data. However, formalizing and testing this notion remained a challenge. This work shows how diffusion models—generative AI techniques producing high-resolution images—operate at different hierarchical levels of features over different time scales of the diffusion process. This phenomenon allows for the generation of images of various classes by recombining low-level features. We study a hierarchical model of data that reproduces this phenomenology and provides a theoretical explanation for this compositional behavior. Overall, the present framework provides a description of how generative models operate, and put forward diffusion models as powerful lenses to probe data structure. Understanding the structure of real data is paramount in advancing modern deep-learning methodologies. Natural data such as images are believed to be composed of features organized in a hierarchical and combinatorial manner, which neural networks capture during learning. Recent advancements show that diffusion models can generate high-quality images, hinting at their ability to capture this underlying compositional structure. We study this phenomenon in a hierarchical generative model of data. We find that the backward diffusion process acting after a time t is governed by a phase transition at some threshold time, where the probability of reconstructing high-level features, like the class of an image, suddenly drops. Instead, the reconstruction of low-level features, such as specific details of an image, evolves smoothly across the whole diffusion process. This result implies that at times beyond the transition, the class has changed, but the generated sample may still be composed of low-level elements of the initial image. We validate these theoretical insights through numerical experiments on class-unconditional ImageNet diffusion models. Our analysis characterizes the relationship between time and scale in diffusion models and puts forward generative models as powerful tools to model combinatorial data properties.

2024

1. 

   Could ChatGPT get an engineering degree? Evaluating higher education vulnerability to AI assistants

   Beatriz Borges , Negar Foroutan , Deniz Bayazit , and 23 more authors

   Proceedings of the National Academy of Sciences, 2024

   Abs PDF

   Universities primarily evaluate student learning through various course assessments. Our study demonstrates that AI assistants, such as ChatGPT, can answer at least 65.8% of examination questions correctly across 50 diverse courses in the technical and natural sciences. Our analysis demonstrates that these capabilities render many degree programs (and their teaching objectives) vulnerable to potential misuse of these systems. These findings call for attention to assessment design to mitigate the possibility that AI assistants could divert students from acquiring the knowledge and critical thinking skills that university programs are meant to instill. AI assistants, such as ChatGPT, are being increasingly used by students in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level Science, Technology, Engineering, and Mathematics (STEM) courses. Specifically, we compile a dataset of textual assessment questions from 50 courses at the École polytechnique fédérale de Lausanne (EPFL) and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass the nonproject assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.

2. 

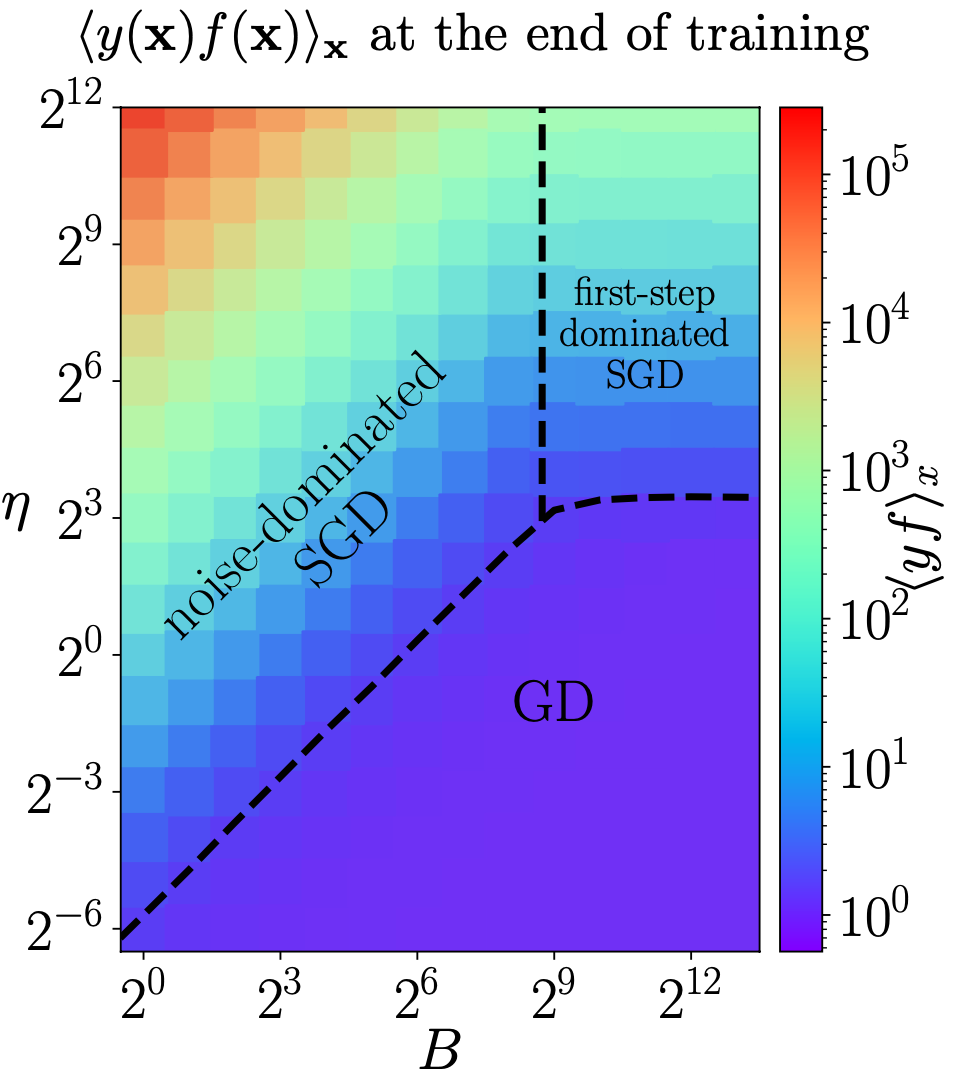   On the different regimes of stochastic gradient descent

   Antonio Sclocchi, and Matthieu Wyart

   Proceedings of the National Academy of Sciences, 2024

   Abs PDF

   

   Modern deep networks are trained with stochastic gradient descent (SGD) whose key hyperparameters are the number of data considered at each step or batch size B, and the step size or learning rate η. For small B and large η, SGD corresponds to a stochastic evolution of the parameters, whose noise amplitude is governed by the “temperature” T≡η/B. Yet this description is observed to break down for sufficiently large batches B≥B∗, or simplifies to gradient descent (GD) when the temperature is sufficiently small. Understanding where these cross-overs take place remains a central challenge. Here, we resolve these questions for a teacher-student perceptron classification model and show empirically that our key predictions still apply to deep networks. Specifically, we obtain a phase diagram in the B-η plane that separates three dynamical phases: i) a noise-dominated SGD governed by temperature, ii) a large-first-step-dominated SGD and iii) GD. These different phases also correspond to different regimes of generalization error. Remarkably, our analysis reveals that the batch size B∗ separating regimes (i) and (ii) scale with the size P of the training set, with an exponent that characterizes the hardness of the classification problem.

2023

1. 

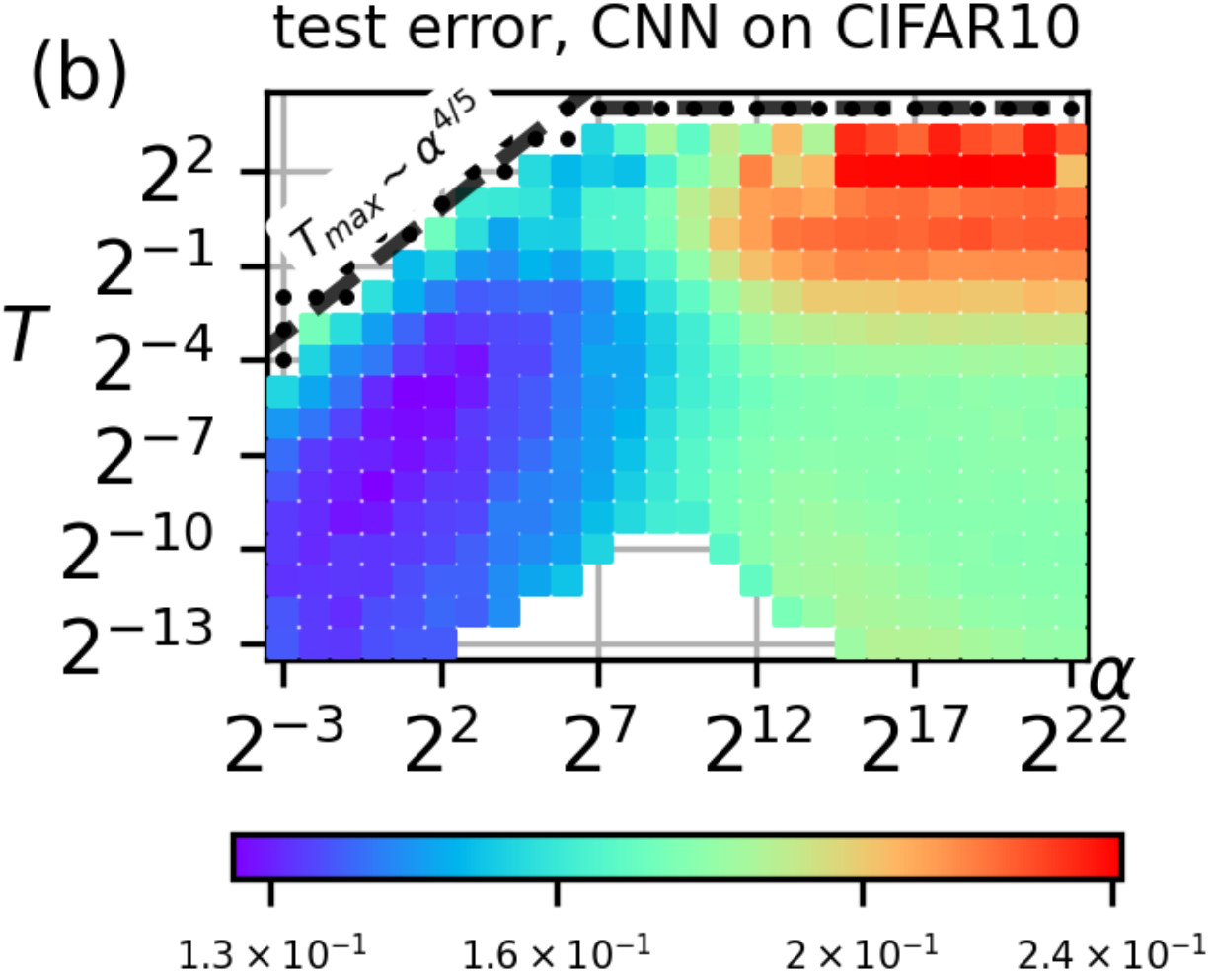   Dissecting the Effects of SGD Noise in Distinct Regimes of Deep Learning

   Antonio Sclocchi, Mario Geiger , and Matthieu Wyart

   In Proceedings of the 40th International Conference on Machine Learning , 23–29 jul 2023

   Abs PDF

   Understanding when the noise in stochastic gradient descent (SGD) affects generalization of deep neural networks remains a challenge, complicated by the fact that networks can operate in distinct training regimes. Here we study how the magnitude of this noise T affects performance as the size of the training set P and the scale of initialization αare varied. For gradient descent, αis a key parameter that controls if the network is lazy’ (α\gg1) or instead learns features (α\ll1). For classification of MNIST and CIFAR10 images, our central results are: *(i)* obtaining phase diagrams for performance in the (α,T) plane. They show that SGD noise can be detrimental or instead useful depending on the training regime. Moreover, although increasing T or decreasing αboth allow the net to escape the lazy regime, these changes can have opposite effects on performance. *(ii)* Most importantly, we find that the characteristic temperature T_c where the noise of SGD starts affecting the trained model (and eventually performance) is a power law of P. We relate this finding with the observation that key dynamical quantities, such as the total variation of weights during training, depend on both T and P as power laws. These results indicate that a key effect of SGD noise occurs late in training, by affecting the stopping process whereby all data are fitted. Indeed, we argue that due to SGD noise, nets must develop a strongersignal’, i.e. larger informative weights, to fit the data, leading to a longer training time. A stronger signal and a longer training time are also required when the size of the training set P increases. We confirm these views in the perceptron model, where signal and noise can be precisely measured. Interestingly, exponents characterizing the effect of SGD depend on the density of data near the decision boundary, as we explain.

2022

1. 

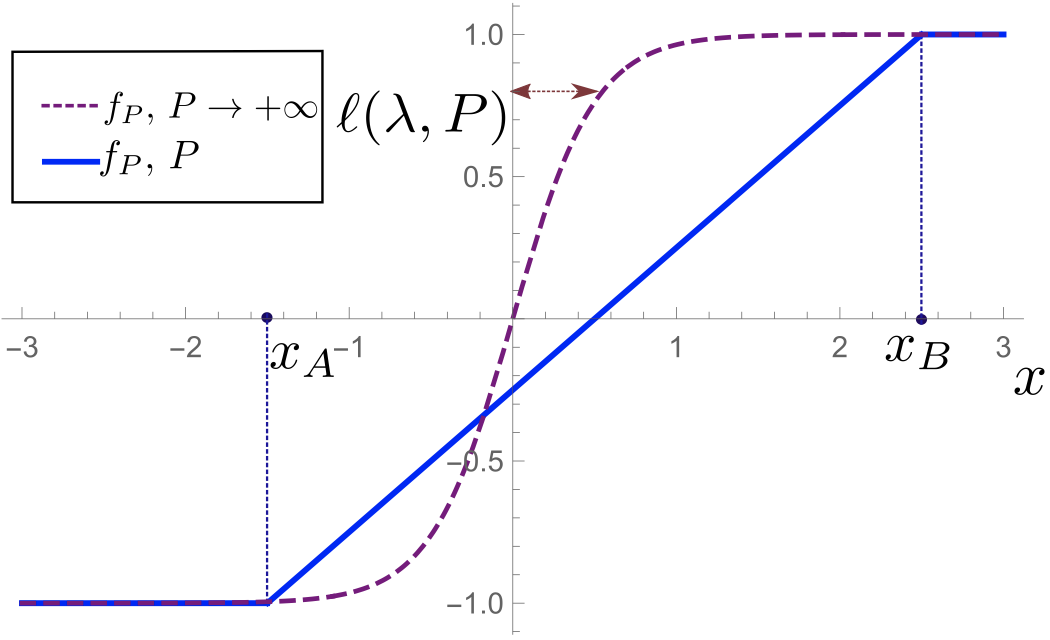   Failure and success of the spectral bias prediction for Laplace Kernel Ridge Regression: the case of low-dimensional data

   Umberto M Tomasini , Antonio Sclocchi, and Matthieu Wyart

   In Proceedings of the 39th International Conference on Machine Learning , 17–23 jul 2022

   Abs PDF

   Recently, several theories including the replica method made predictions for the generalization error of Kernel Ridge Regression. In some regimes, they predict that the method has a ‘spectral bias’: decomposing the true function f^* on the eigenbasis of the kernel, it fits well the coefficients associated with the O(P) largest eigenvalues, where P is the size of the training set. This prediction works very well on benchmark data sets such as images, yet the assumptions these approaches make on the data are never satisfied in practice. To clarify when the spectral bias prediction holds, we first focus on a one-dimensional model where rigorous results are obtained and then use scaling arguments to generalize and test our findings in higher dimensions. Our predictions include the classification case f(x)=sign(x_1) with a data distribution that vanishes at the decision boundary p(x)∼x_1^χ. For χ>0 and a Laplace kernel, we find that (i) there exists a cross-over ridge λ^*_d,χ(P)∼P^-\frac1d+χ such that for λ≫λ^*_d,χ(P), the replica method applies, but not for λ≪λ^*_d,χ(P), (ii) in the ridge-less case, spectral bias predicts the correct training curve exponent only in the limit d→∞.

2. 

   High-dimensional optimization under nonconvex excluded volume constraints

   Antonio Sclocchi, and Pierfrancesco Urbani

   Phys. Rev. E, Feb 2022

   Abs PDF

   We consider high-dimensional random optimization problems where the dynamical variables are subjected to nonconvex excluded volume constraints. We focus on the case in which the cost function is a simple quadratic cost and the excluded volume constraints are modeled by a perceptron constraint satisfaction problem. We show that depending on the density of constraints, one can have different situations. If the number of constraints is small, one typically has a phase where the ground state of the cost function is unique and sits on the boundary of the island of configurations allowed by the constraints. In this case, there is a hypostatic number of marginally satisfied constraints. If the number of constraints is increased one enters a glassy phase where the cost function has many local minima sitting again on the boundary of the regions of allowed configurations. At the phase transition point, the total number of marginally satisfied constraints becomes equal to the number of degrees of freedom in the problem and therefore we say that these minima are isostatic. We conjecture that by increasing further the constraints the system stays isostatic up to the point where the volume of available phase space shrinks to zero. We derive our results using the replica method and we also analyze a dynamical algorithm, the Karush-Kuhn-Tucker algorithm, through dynamical mean-field theory and we show how to recover the results of the replica approach in the replica symmetric phase.

2021

1. 

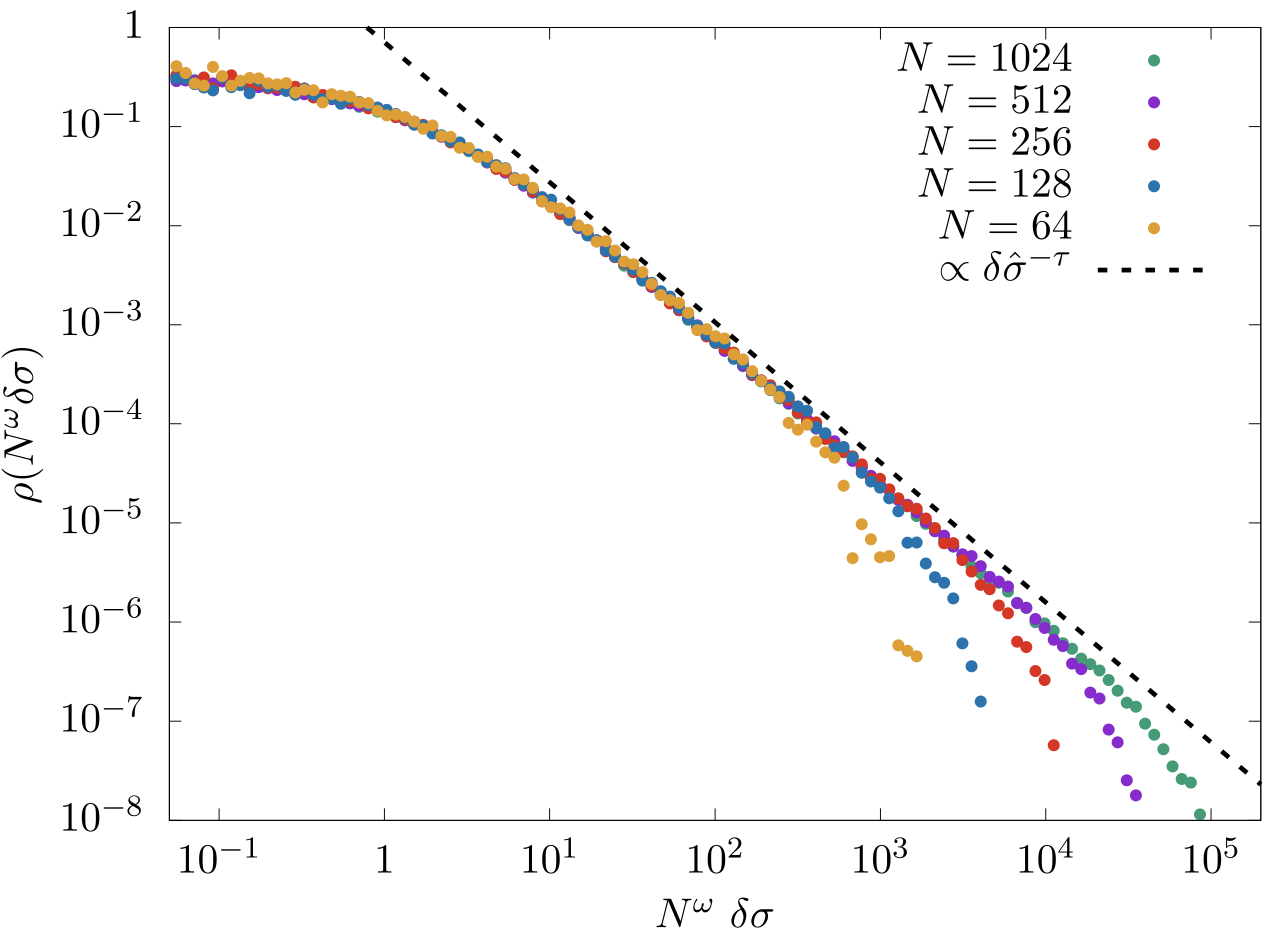   Surfing on minima of isostatic landscapes: avalanches and unjamming transition

   Silvio Franz , Antonio Sclocchi, and Pierfrancesco Urbani

   Journal of Statistical Mechanics: Theory and Experiment, Feb 2021

   Abs PDF

   Recently, we showed that optimization problems, both in infinite as well as in finite dimensions, for continuous variables and soft excluded volume constraints, can display entire isostatic phases where local minima of the cost function are marginally stable configurations endowed with non-linear excitations [1, 2]. In this work we describe an athermal adiabatic algorithm to explore with continuity the corresponding rough high-dimensional landscape. We concentrate on a prototype problem of this kind, the spherical perceptron optimization problem with linear cost function (hinge loss). This algorithm allows to ‘surf’ between isostatic marginally stable configurations and to investigate some properties of such landscape. In particular we focus on the statistics of avalanches occurring when local minima are destabilized. We show that when perturbing such minima, the system undergoes plastic rearrangements whose size is power law distributed and we characterize the corresponding critical exponent. Finally we investigate the critical properties of the unjamming transition, showing that the linear interaction potential gives rise to logarithmic behavior in the scaling of energy and pressure as a function of the distance from the unjamming point. For some quantities, the logarithmic corrections can be gauged out. This is the case of the number of soft constraints that are violated as a function of the distance from jamming which follows a non-trivial power law behavior.

2. 

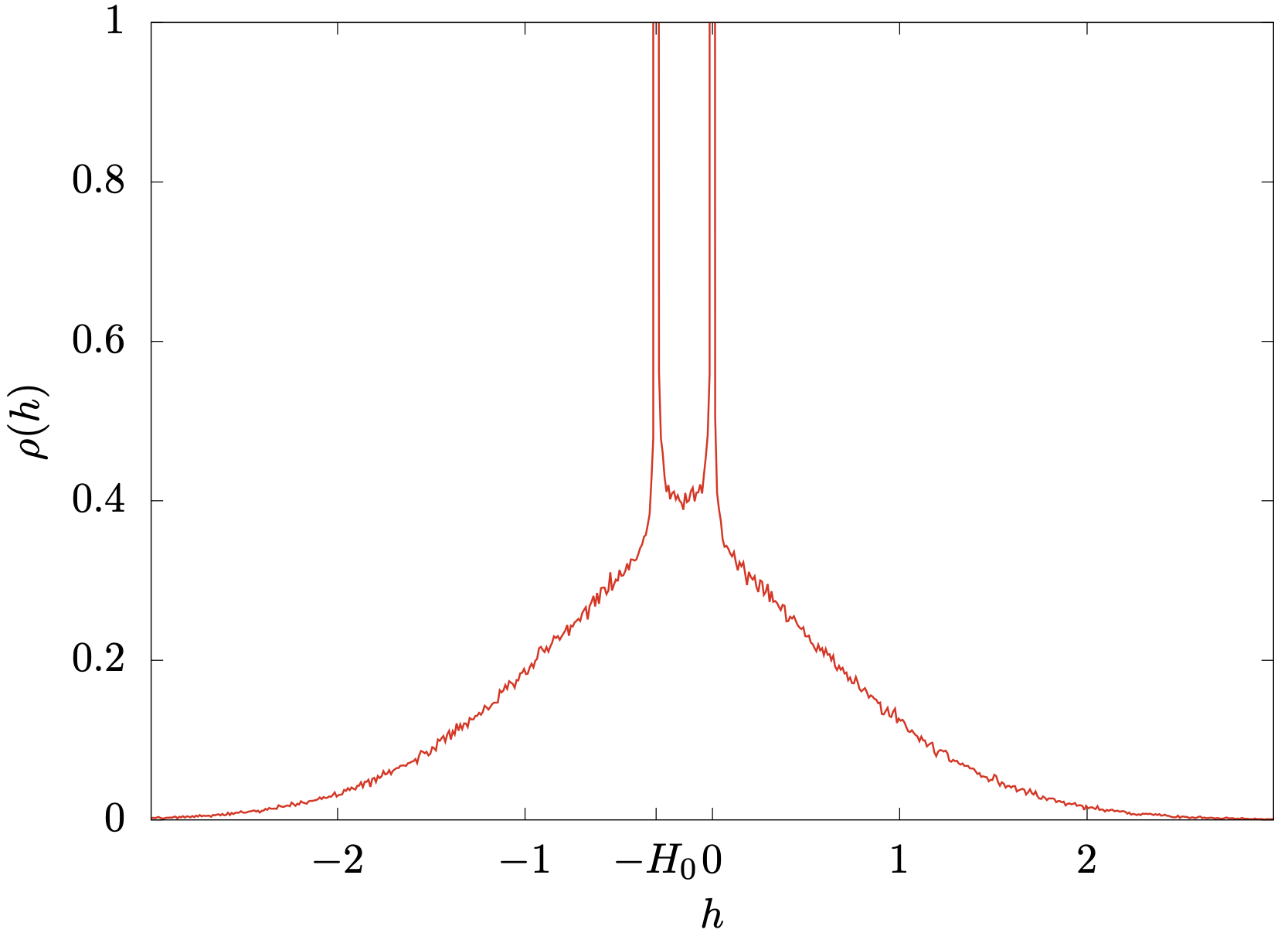   Proliferation of non-linear excitations in the piecewise-linear perceptron

   Antonio Sclocchi, and Pierfrancesco Urbani

   SciPost Phys., Feb 2021

   Abs PDF

   We investigate the properties of local minima of the energy landscape of a continuous non-convex optimization problem, the spherical perceptron with piecewise linear cost function and show that they are critical, marginally stable and displaying a set of pseudo- gaps, singularities and non-linear excitations whose properties appear to be in the same universality class of jammed packings of hard spheres. The piecewise linear perceptron problem appears as an evolution of the purely linear perceptron optimization problem that has been recently investigated in [1]. Its cost function contains two non-analytic points where the derivative has a jump. Correspondingly, in the non-convex/glassy phase, these two points give rise to four pseudogaps in the force distribution and this induces four power laws in the gap distribution as well. In addition one can define an extended notion of isostaticity and show that local minima appear again to be isostatic in this phase. We believe that our results generalize naturally to more complex cases with a proliferation of non-linear excitations as the number of non-analytic points in the cost function is increased.

2020

1. 

   Critical energy landscape of linear soft spheres

   Silvio Franz , Antonio Sclocchi, and Pierfrancesco Urbani

   SciPost Phys., Feb 2020

   Abs PDF

   We show that soft spheres interacting with a linear ramp potential when overcompressed beyond the jamming point fall in an amorphous solid phase which is critical, mechanically marginally stable and share many features with the jamming point itself. In the whole phase, the relevant local minima of the potential energy landscape display an isostatic contact network of perfectly touching spheres whose statistics is controlled by an infinite lengthscale. Excitations around such energy minima are non-linear, system spanning, and characterized by a set of non-trivial critical exponents. We perform numerical simulations to measure their values and show that, while they coincide, within numerical precision, with the critical exponents appearing at jamming, the nature of the corresponding excitations is richer. Therefore, linear soft spheres appear as a novel class of finite dimensional systems that self-organize into new, critical, marginally stable, states.

2019

1. 

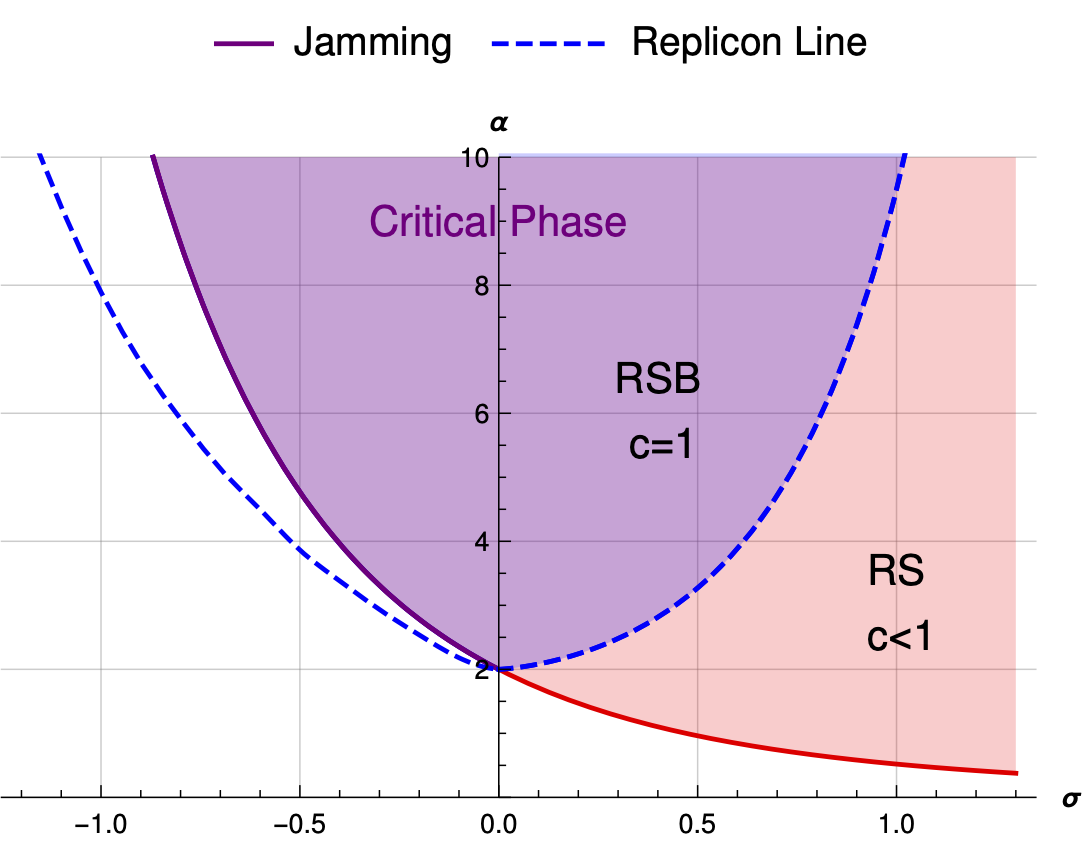   Critical Jammed Phase of the Linear Perceptron

   Silvio Franz , Antonio Sclocchi, and Pierfrancesco Urbani

   Phys. Rev. Lett., Sep 2019

   Abs PDF

   Criticality in statistical physics naturally emerges at isolated points in the phase diagram. Jamming of spheres is not an exception: varying density, it is the critical point that separates the unjammed phase where spheres do not overlap and the jammed phase where they cannot be arranged without overlaps. The same remains true in more general constraint satisfaction problems with continuous variables where jamming coincides with the (protocol dependent) satisfiability transition point. In this work we show that by carefully choosing the cost function to be minimized, the region of criticality extends to occupy a whole region of the jammed phase. As a working example, we consider the spherical perceptron with a linear cost function in the unsatisfiable jammed phase and we perform numerical simulations which show critical power laws emerging in the configurations obtained minimizing the linear cost function. We develop a scaling theory to compute the emerging critical exponents.

2017

1. 

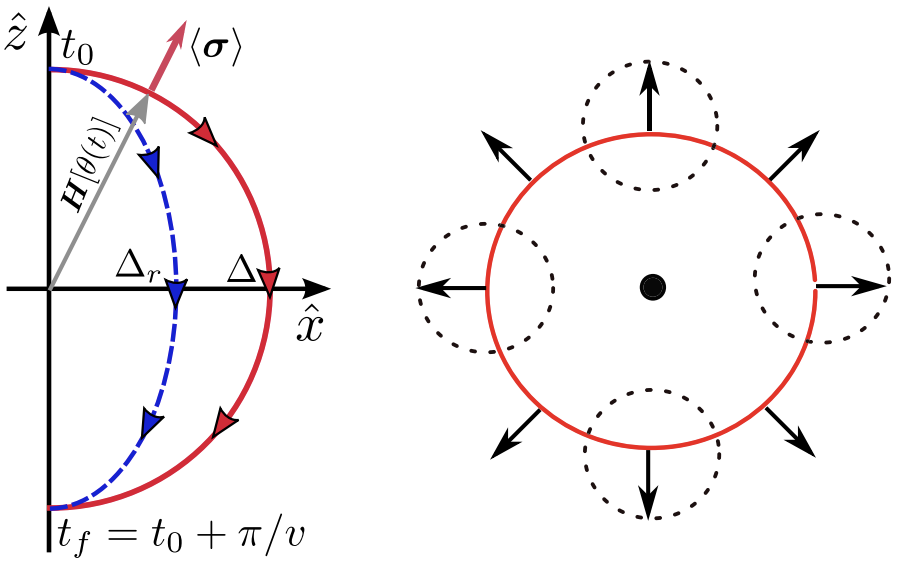   Topology of a dissipative spin: Dynamical Chern number, bath-induced nonadiabaticity, and a quantum dynamo effect

   Loı̈c Henriet , Antonio Sclocchi, Peter P. Orth , and 1 more author

   Phys. Rev. B, Feb 2017

   Abs PDF

   We analyze the topological deformations of a spin-1/2 in an effective magnetic field induced by an ohmic quantum dissipative environment at zero temperature. From Bethe Ansatz results and a variational approach, we confirm that the Chern number is preserved in the delocalized phase for α<1. We report a divergence of the Berry curvature at the equator when \alpha_c=1 that appears at the localization Kosterlitz-Thouless quantum phase transition in this model. Recent experiments in quantum circuits have engineered non-equilibrium protocols in time to access topological properties at equilibrium from the measure of the (quasi-)adiabatic out-of-equilibrium spin expectation values. Applying a numerically exact stochastic Schrödinger equation we find that, for a fixed sweep velocity, the bath induces a crossover from (quasi-)adiabatic to non-adiabatic dynamical behavior when the spin bath coupling increases. We also investigate the particular regime H/\omega_c ≪v/H ≪1, where the dynamical Chern number observable built from out-of-equilibrium spin expectation values vanishes at α=1/2. In this regime, the mapping to an interacting resonance level model enables us to characterize the evolution of the dynamical Chern number in the vicinity of α=1/2. Then, we provide an intuitive physical explanation of the breakdown of adiabaticity in analogy to the Faraday effect in electromagnetism. We demonstrate that the driving of the spin leads to the production of a large number of bosonic excitations in the bath, which in return strongly affect the spin dynamics. Finally, we quantify the spin-bath entanglement and build an analogy with an effective model at thermal equilibrium.